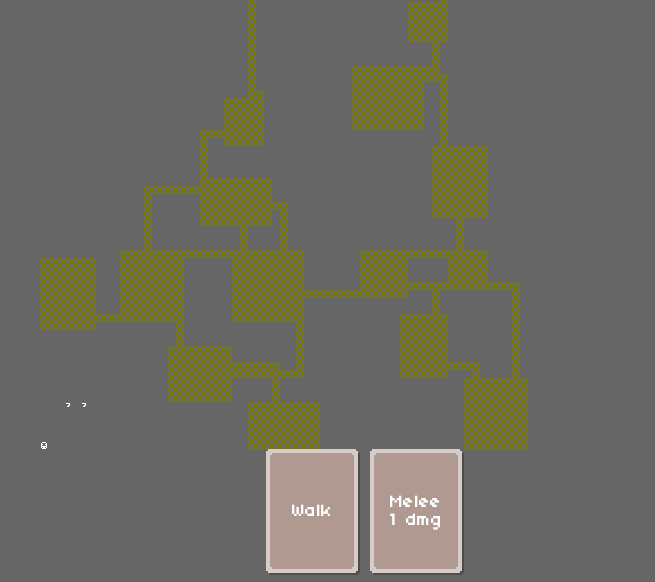
Last time we have left of our dungeon generation with some hardcoded room positions. This time we will improve on that by adding some proper randomization.
The complete code for this part can be found here: https://github.com/maciekglowka/hike_deck/tree/part_10
RoomGenerator
We are going to take a bit of a similar approach, as with the tunnel creation. We will make a common trait for the room generation process, so we can easily swap different algorithms. (like different tunneler types previously). That should allow us in the future to be a bit more flexible with our board designs and include special areas like temples or arenas next to the typical chambers.
So, the trait:
pub trait RoomGenerator {
fn generate(&self) -> GeneratorResult;
}
pub struct GeneratorResult {
pub rooms: Vec<Room>,
pub connections: Vec<(usize, usize)>
}
The trait defines only a single method - one creating the room layout. As you can see in the result, apart from the rooms, we also include the desired connections between them. This way we will ensure that our chambers are logically joined together - depending on the algorithm's rules.
Now let's move to the first (and for now only) implementation. We are going to take a very simple bubbling approach here:
- Create a random room at
(0, 0) and push it into a list
- Pick a room from the list as a reference (at first only one will be available)
- Find a random new room around the reference one
- Make sure the new room is valid (eg. does not overlap with any other)
- Connect the two rooms
- From time to time add a second random tunnel
- Go back to 2. until we hit the target room count
In order to control our randomization a little bit, we will provide the room generator with some initial parameters - like the desired room count, size ranges etc.
Here is the initial code (I hope the comments make it clear enough):
pub struct BubbleGenerator {
pub room_count: (u32, u32),
pub room_size: (u32, u32),
pub room_padding: Option<u32>,
pub extra_connection_chance: f64
}
impl BubbleGenerator {
fn random_dim(&self) -> (i32, i32) {
let mut rng = thread_rng();
(
rng.gen_range(self.room_size.0..=self.room_size.1) as i32,
rng.gen_range(self.room_size.0..=self.room_size.1) as i32
)
}
}
impl RoomGenerator for BubbleGenerator {
fn generate(&self) -> GeneratorResult {
let mut rng = thread_rng();
let mut connections = Vec::new();
let (w, h) = self.random_dim();
let mut rooms = vec![
Room::new(
Vector2Int::new(0, 0),
Vector2Int::new(w, h)
)
];
let max_dist = self.room_size.1 as i32;
let count = rng.gen_range(self.room_count.0..=self.room_count.1);
for _ in 0..=count {
loop {
let prev_idx = rng.gen_range(0..rooms.len());
let centre = rooms[prev_idx].centre();
let a = Vector2Int::new(
rng.gen_range(centre.x - max_dist..=centre.x + max_dist),
rng.gen_range(centre.y - max_dist..=centre.y + max_dist)
);
let (w, h) = self.random_dim();
let b = Vector2Int::new(
a.x + *[-w, w].choose(&mut rng).unwrap(),
a.y + *[-h, h].choose(&mut rng).unwrap()
);
let r = Room::new(a, b);
if rooms.iter().any(|other| r.intersects(other, self.room_padding)) {
continue;
}
connections.push((prev_idx, rooms.len()));
if rng.gen_bool(self.extra_connection_chance) {
connections.push((rng.gen_range(0..rooms.len()), rooms.len()));
}
rooms.push(Room::new(a, b));
break;
}
}
GeneratorResult { rooms, connections }
}
}
In order for the above to work, we also have to add two more helper methods to the Room struct:
impl Room {
pub fn centre(&self) -> Vector2Int {
Vector2Int::new((self.b.x+self.a.x) / 2, (self.b.y+self.a.y) / 2)
}
pub fn intersects(&self, other: &Room, border: Option<u32>) -> bool {
let b = match border {
Some(a) => a as i32,
None => 0
};
!(
other.a.x > self.b.x + b ||
other.b.x < self.a.x - b ||
other.a.y > self.b.y + b ||
other.b.y < self.a.y - b
)
}
}
The border parameter in the intersects method allows us to add some extra spacing around the rooms - if a positive value is provided. But you may also omit it for more organic layouts.
Now let's change the Area struct so it accepts the RoomGenerator object (as we did with the tunneler):
pub struct Area {
pub rooms: Vec<Room>,
pub paths: Vec<Vec<Vector2Int>>,
pub tunneler: Box<dyn Tunneler>,
pub room_generator: Box<dyn RoomGenerator>
}
impl Area {
pub fn new(tunneler: Box<dyn Tunneler>, room_generator: Box<dyn RoomGenerator>) -> Self {
Area { rooms: Vec::new(), paths: Vec::new(), tunneler, room_generator }
}
pub fn generate_rooms(&mut self) {
let result = self.room_generator.generate();
self.rooms = result.rooms;
self.paths = result.connections.iter()
.map(|a| self.join_rooms(&self.rooms[a.0], &self.rooms[a.1]))
.collect();
}
}
One last thing left to do - include the generator object when spawning the board. You can fiddle with it's parameters and see how it affects the dungeon layout. You can even go further and use different parameters for each of the areas.
pub fn spawn_map(
mut commands: Commands,
mut current: ResMut<CurrentBoard>
) {
let mut dungeon = Dungeon::new(2);
for idx in 0..4 {
let tun = match idx % 2 {
0 => Box::new(tunneler::LShapeTunneler) as Box<dyn tunneler::Tunneler>,
_ => Box::new(tunneler::RandomTunneler) as Box<dyn tunneler::Tunneler>
};
let gen = Box::new(room::BubbleGenerator {
room_count: (3, 5),
room_size: (4, 8),
room_padding: Some(2),
extra_connection_chance: 0.25
}) as Box<dyn room::RoomGenerator>;
dungeon.add_area(Area::new(tun, gen))
}
dungeon.generate();
current.tiles = HashMap::new();
for v in dungeon.to_tiles() {
let tile = commands.spawn((
Position { v },
Tile
))
.id();
current.tiles.insert(v, tile);
}
}
Anyways, after running the game now you should already be able to see something that might resemble a proper game map. Probably our characters will be outside of the board now, but we will handle that in the next part (or the one after that ;)